第238回英国の大航海時代と数学者［後編］

前回のコラムで大航海時代に対数が生まれたこと、つまり、航路の位置や距離の計測には複雑な球面三角法が使われ、その計算を簡易化するために対数が生まれたことをお話ししました。今回も科学博物館内の数学ギャラリーの展示から、数学者の貢献をご紹介しようと思います。17世紀後半になると、大砲の弾道や物質の化学変化を正確に測定したいというニーズが増え、それらの複雑な計算を簡易化するため再び対数が注目されました。

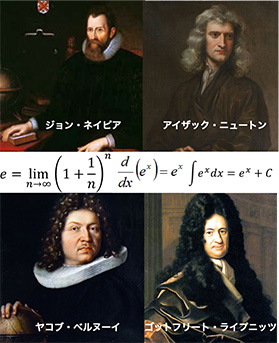微分積分に関わる著名な数学者たち

運動体の速度を微分すれば加速度、積分すれば距離になりますが、微分積分の計算はとても複雑です。その簡易化のため、前回登場した数学者ジョン・ネイピアに由来する自然対数の底、ネイピア数eが使われます。ネイピア数は17世紀にスイスの数学者ヤコブ・ベルヌーイが金利の複利計算をしている過程で、複利回数を無限に増やすとe=2.71828…倍に元利金が収束することを見つけました。ベルヌーイは独数学者ゴットフリート・ライプニッツと共に微分積分学を発展させ、同じころ、英数学者ニュートンも微分積分を思いつきました。

ニュートンの論文（写真左）とマンチェスター大学の微分解析機（同右） ※科学博物館蔵

実際のところ、自然界の現象や人間の経済活動には指数的に変動するものが多く、その変動の勢いや面積を測定するには微分積分が使われます。その際、このネイピア数eを使えば計算をかなり簡易化できます。指数関数y=e^xを微分しても、また積分してもその値がe^xのまま変わらないというのがネイピア数eの特質だからです。

宝くじ計算機「グィネヴィア」 ※科学博物館蔵宝くじ計算機「グィネヴィア」 ※科学博物館蔵

科学博物館の数学ギャラリーに展示されている、1736年出版のニュートンの論文「流率と無限級数の方法について」には、微分積分の考え方の基礎が書かれています。その隣にあるのがマンチェスター大学の微分解析機で、熱伝導や伝送線路、ウラン濃縮（広島に落とされた原爆の模擬計算）の計算に使われたそうです。確かに熱いお湯が冷めるときの温度変化や放射性物質の放射線量は指数関数で表現できると昔、本で読みました。

保険料算出の基となる生命表の計算機（19世紀） ※科学博物館蔵

また、ネイピア数eはランダムな数字を作り出したり、大数の法則を把握する確率密度関数の計算にも使われます。展示されているアーサー王の妃グィネヴィアと命名された英国公営の宝くじ機や、生命保険料の基となる生命表を計算する機械も、ネイピア数e無しには計算できません。天井には流体力学で計算された飛行機の気流が、有名建築家ザハ・ハディット氏によりデザインされており、微分、積分、いい気分の世界が広がっています。

ザハ・ハディット氏設計の流体力学モデル ※科学博物館蔵